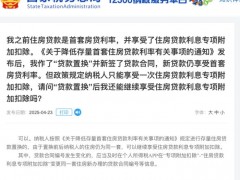
1)设CE的长为x千米,依据题意得
1.6+1+x+1=2(3-2×0.5)
解得x=0.4,即CE的长为0.4千米.
(2)若步行路线为A—D—C—B—E—A(或A—E—B—C—D—A),
则所用时间为 (1.6+1+1.2+0.4+1)+3×0.5=4.1(小时);
若步行路线为A—D—C—E—B—E—A(或A—E—B—E—C—D—A),
则所用时间为 (1.6+1+0.4+0.4×2+1)+3×0.5=3.9(小时).
故步行路线应为A—D—C—E—B—E—A(或A—E—B—E—C—D—A)
顶一下
如图,某风景区有一古塔AB,在塔的北面有一建筑物,冬至日的正午光线与水平面的夹角是30°,此时塔在
| 2.6. |
| 试题分析:连接OA,由垂径定理易得出AD的长度,在Rt△OAD中,可用半径表示出OD的长,根据勾股定理即可求出半径的长度. 试题解析:连接OA;
Rt△OAD中,AD= AB=1米; 设⊙O的半径为R,则OA=OC=R,OD=5-R; 由勾股定理,得:OA 2 =AD 2 +OD 2 ,即: R 2 =(5-R) 2 +12,解得R=2.6(米); 考点: 垂径定理的应用. |
如图,某风景区的沿湖公路 AB =3千米, BC =4千米, CD =12千米, AD =13千米,其中 AB ^ BC ,图中阴影
如图,过点D作DF⊥AB,垂足为F,
∵AB⊥BC,CD⊥BC,
∴四边形BCDF的矩形,
∴BC=DF,CD=BF,
设AB=x米,
在Rt△ABE中,∠AEB=∠BAE=45°,
∴BE=AB=x,
在Rt△ADF中,
∠ADF=30°,AF=AB-BF=x-3,
∴DF=AF•cot30°= 根号3(x-3),
∵DF=BC=BE+EC,
∴ 根号3(x-3)=x+15,
解得x=12+ 9根号3,
答:塔AB的高度(12+ 9根号3)米.
望采纳~
数学:如图,某风景区的旅游路线示意图,其中B,C,D...
| 0.4 |
| 连接AC,在直角△ABC中,已知AB,BC可以求AC,根据AC,CD,AD的长度符合勾股定理确定AC⊥CD,则可计算△ACD的面积, 又因为△ACD的面积可以根据AD边和AD边上的高求得,故根据△ACD的面积可以求得C到AD的最短距离,即△ACD中AD边上的高. 解:连接AC,
在直角△ABC中,AB=3km,BC=4km,则AC= =5km, ∵CD=12km,AD=13km,故存在AD 2 =AC 2 +CD 2 ∴△ACD为直角三角形,且∠ACD=90°, ∴△ACD的面积为 ×AC×CD=30km 2 , ∵AD=13km,∴AD边上的高,即C到AD的最短距离为 km, 游艇的速度为11 km/小时, 需要时间为 小时=0.4小时. 故答案为 0.4. |
:(1)设CE长为xkm,
x+1.6+1+1=(3-1)×2,
x=0.4;
(2)路线是:由图可知最佳路线为ADCEBEA,
路程为:1.6+1+0.4+0.4+0.4+1=4.8km,
此路程线路为最短.
答:(1)CE长为0.4km;(2)路线是:最佳路线为ADCEBEA.
以上就是关于如图是某风景区的旅游路线示意图,其中B、C、D为风景点,E为两条路的交叉点,图中数全部的内容,如果了解更多相关内容,可以关注我们,你们的支持是我们更新的动力!